Merge sort is another prevalent and efficient algorithm. It is a divide-and-conquer algorithm in Python with more efficient characteristics for large lists. It does not depend on any ineffective decisions that lead to flawed runtimes.
This article on merge sort in Python will discuss implementing the algorithm with some Python programs.
The Concept of Merge Sort in Python:
The two algorithms, namely quick sort and Merge sort, have almost the same concept of divide and conquer. The merge sort algorithm is one of the most widely used and easy algorithms for sorting.
When it finds a data structure, it splits the provided list into two halves and then combines the two sorted halves. Users can use the merge() function to merge the two halves.
It will split the sub-lists again and again into further halves until users get a single element from the list of elements. Then users can merge the pair of one-element lists into two-element lists, sorting these items in the process.
They then combine the sorted two-element pairs into a four-element list and continue the merging process until they get the sorted list.
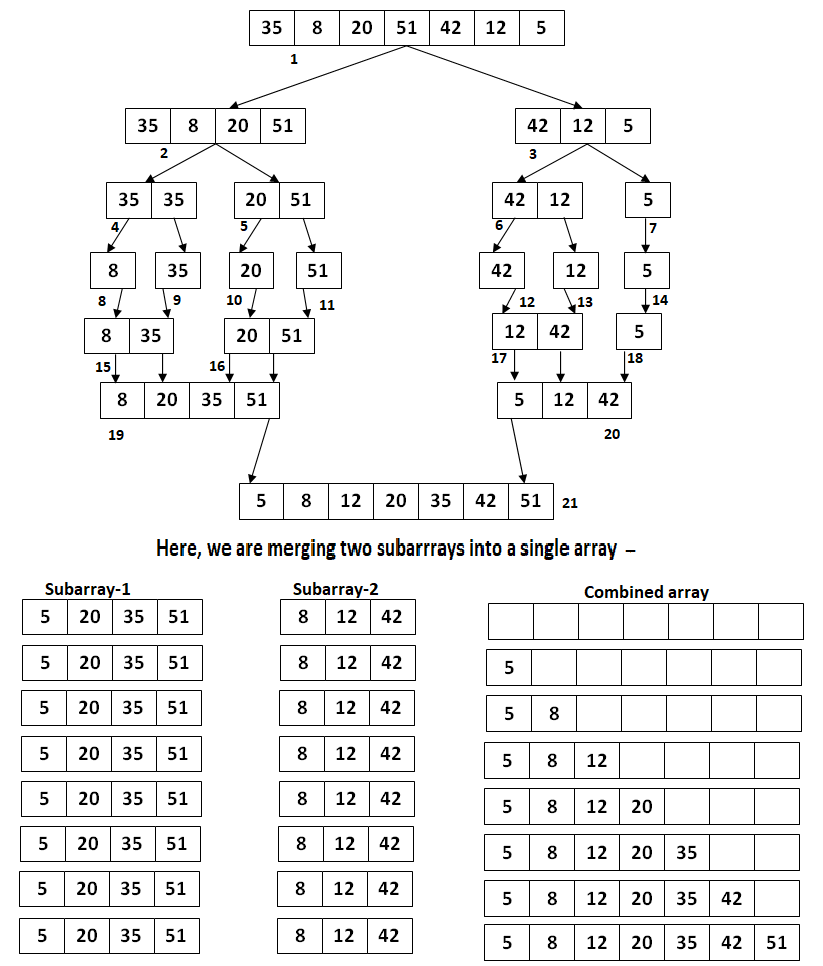
Let us consider an example of merge sort using two sub-lists:
A: [3, 6, 8, 10]
B : [2, 7, 9]
First, users have to divide a given list into two halves. These two halves can be equal. If they cannot split the list into equal parts, it will not matter.
Users can implement the merge sort algorithm using two ways. These are the top-down approach and bottom-up approach. Here, we are using the top-down approach in this Python example. The following sections of this article will discuss the bottom-up approach, which gives more optimization to the Python code.
The primary function of the merge sort algorithm is how users combine the two sorted sub-lists into one list. Let us merge the two sorted merge lists using the following steps:
A : [3, 6, 8, 10]
B : [2, 7, 9]
Sorted : empty
First, users observe the first item of both lists. Here, list B has "2" as the first item, and list A has "3." We are adding 1, which is smaller than that of list A into the sorted list and moving forward in the B list.
A : [3, 6, 8, 10]
B : [2, 7, 9]
Sorted : 2
Now we move forward to the next pair of elements, "3" and "7." "3" of list A is smaller, so we are adding it to the sorted list and moving forward with the sub-lists.
A : [3, 6, 8, 10]
B : [2, 7, 9]
Sorted : 2 3
We will continue the process until we end up with the sorted list of {2, 3, 6, 7, 8, 9, 10}.
Note: Always remember these two particular cases:
When both the sub-lists have the same elements:
In such a case, users can select any f the sub-lists and add the items of that list to the sorted list. Generally, users can proceed with both sublists and add the items to their sorted list.
Empty sub-lists:
When users have a sub-list that contains no element, they can run out of the sublist and add the items of the second sub-list after the other.
Users can sort the items in any order. Either they can merge sort in Python using the ascending order or readily sort in descending order.
Code Snippet:
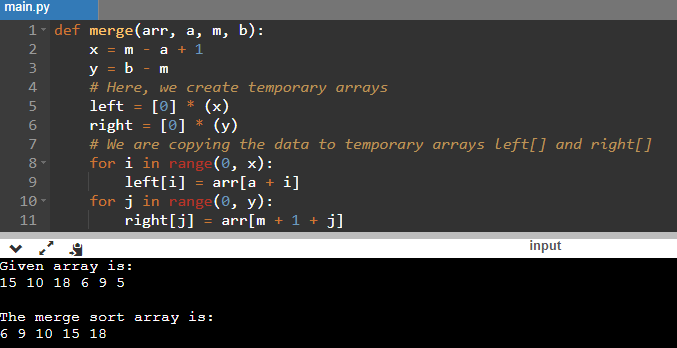
def merge(arr,a,m,b):
x=m - a + 1
y=b - m
# Here,we create temporary arrays
left=[0] * (x)
right=[0] * (y)
# We are copying the data to temporary arrays left[] and right[]
for i in range(0,x):
left[i]=arr[a + i]
for j in range(0,y):
right[j]=arr[m + 1 + j]
# We are merging the temporary arrays back into arr[l..r]
i=0
j=0
k=a
while i < x and j < y:
if left[i] <= right[j]:
arr[k]=left[i]
i += 1
else:
arr[k]=right[j]
j += 1
k += 1
# we are copying the remaining items of left[],if there are any
while i < x:
arr[k]=left[i]
i += 1
k += 1
# we are copying the remaining items of right[],if there are any
while j < y:
arr[k]=right[j]
j += 1
k += 1
def demo(arr,a,b):
if a < b:
m=a+(b-a)//2
demo(arr,a,m)
demo(arr,m+1,b)
merge(arr,a,m,b)
arr=[15,10,18,6,9,5]
i=len(arr)
print("Given array is: ")
for i in range(i):
print("%d" % arr[i],end="")
demo(arr,0,i-1)
print("\n\nThe merge sort array is:")
for i in range(i):
print("%d" % arr[i],end="")
Output:
Explanation:
The merge(arr, a, m, b) is the critical process that accepts that the process has merged and sorted the arr[a..b] and arr[m+1..b] into the two sorted sub-arrays into one.
Time Complexity and auxiliary space of merge sort in Python:
O(n*log(n)) and O(n)