SAP SCM (Supply Chain Management)
Definition or Meaning - What is SAP SCM?
Full form or SAP SCM stands for (Supply Chain Management), an important part of the group of SAP customized solutions, boasts of the distinction of being one of the most impact full SCM software applications in the market. It is specifically designed to maintain organization relationships with customers and suppliers; streamline the processes of planning, distribution, inventory and transportation; and effectively control and manage the entire supply chain to address customer expectations and perform to the optimum levels.
SAP SCM plays an important role in enabling an organization coordinate its entire supply chain process in accordance to the dynamism in the environment - thus helping customers, suppliers, manufactures, retailers, business partners and other global connections to stay connected and generate result-oriented solutions.
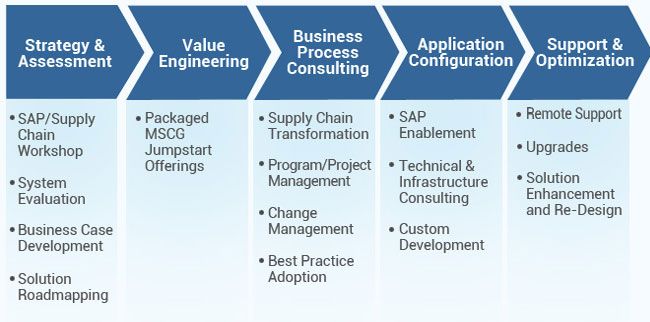
The components of SAP SCM are:
- SC Collaboration - helps in making collaborative forecasts and agreements.
- SC Planning - generates tactical and operational plans on the basis of current, relevant data.
- SC coordination - coordinates through the exchange of data and information between departments.
- SC Execution - ensures that well conceived plans are executed to cater to customer orders in the best possible manner.
SAP SCM primary applications are segregated as:
- General areas of SAP
- SAP Extended Warehouse
- SAP Transportation Management
- Advanced Planning and Optimization
- Supply chain management
- SAP supply network collaboration
- Forecasting and Replenishment
Across the world, organizations are facing enormous pressures for reducing costs while improving customer services and increasing innovation as well as responsiveness. SAP SCM enables the planning, collaboration, execution and coordination of the supply network, and empowers them to adopt smarter supply chain processes and deal with their ever-changing competitive environment.
The benefits of integrating this module include:
- Smarter planning and execution of SAP supply chain solutions for meeting customer demands.
- Effective streamlining of internal departments with their external partners, total control of Business Processes and smoother operations for more efficient and profitable running or organizations.
- Competent forecasting and handling of sudden changes in demand and supply.
- Provision of vital business information to all key stakeholders located across the network.
- Improved collaboration and better management of multiple lines of business.
- Real - time decision making for early execution across the supply chain.
- Central management and optimization of Inventory, order fulfillment and shipping.
- Proper handling of supply chain disruptions and maintenance of the supply chain’s integrity and so forth.
Read Next:
SAP SCM (Supply Chain Management) Certification Fee and Course Duration in India
SAP SCM (Supply Chain Management) Module Scope and Career Opportunity
Tutorials
- SAP SCM (Supply Chain Management) Module Scope, Career and Consultant
Scope and Opportunity of a Career in SAP Supply Chain Management (SCM)The SAP SCM is most suitable for: Project leaders, project team members, SAP consultants, super users, sales consultant, and those ... - SAP SCM (Supply Chain Management) Certification Fee and Course Duration in India
SAP SCM (Supply Chain Management) courses are modeled to extend the advantage of power packed SAP solutions to their audience and enhance their abilities for handling the tasks related to planning, lo ... - Job Profile & Salary Package for SAP SCM (Supply Chain Management Consultant
SAP SCM is a customized product which covers the functionalities of Supply chain network, planning, coordination, procurement, advanced planning and optimization. The certification in course opens ... - System Landscape Copy for SAP SCM
You want to copy a productive SAP solution landscape to create a non-productive system landscape for testing, quality assurance or other purposes. Or you want to copy your productive landscape onto a ... - Qualifications and Skills requires to become a SAP SCM (Supply Chain Management) Consultant
Who can pursue this course? SAP SCM is designed to automate the supply chain management process and thus synchronize all the functionalities of supply chain and meet the expected customers ... - Creation of inbound delivery during two-step stock transfers
If you activate service parts management (SPM) in Release ECC 6.00 or higher, the system can automatically create an inbound delivery during two-step stock transfers. You can use the inbound delivery ... - How to create and use Expected Goods Receipt?
Hello Experts,I am having this queries, kindly share your views on it.How do I use the expected goods receipt?How can I create an expected goods receipt?Thanks in advance. ... - CNTL_ERROR in Interactive Demand Planning
RAISE_EXCEPTIONWhen we perform user interaction such as drill down, grouping, pivot sorting after loading the data into planning grid in transaction /n/sapapo/sdp94 (interactive demand planning) Short ...  Define Graphic Profile in SAP
Define Graphic Profile in SAP
In this SAP tutorial, users will learn the step-by-step process to define a new graphic profile in your SAP system will proper screenshot. What is Graphic Profile in SAP? The SAP graphics profil ...- Define Putaway Control Indicator
This SAP SCM Extended Warehouse Management tutorial, explains to the users the step-by-step procedure to define a Putaway Control Indicator in the SAP system with proper screenshots of every step perf ... - Determine Alert Priority in SAP
This SAP SCM tutorial explains the SAP users the step-by-step procedure to determine Alert Priority in the SAP system with proper screenshots. What is Alert Priority in SAP? The Alert Priority i ... - Create Planned Order Creation
In this SAP SCM tutorial, you will learn the step y step procedure to create Planned Order Creation in your SAP system with proper screenshots at every step. What is Planned Order Creatio ...