When it comes to large numbers, often, users fail to solve exponents like they generally do multiplication in Python. The term "2^3" becomes much easy for sure as users can multiply the "2" three times and get the result.
But it will not work when users have to code it in Python. So, they need a proper method to solve the exponents. This article will provide the techniques to deal with exponential numbers and a brief explanation of exponents in Python with the following code snippets.
What are exponents?
In simple terms, we can say that an exponent is a number or letter that defines how many times a number or any mathematical expression will get multiplied. Users usually write the exponent of a number above it (in its power), i.e., they can write it to the top right-most side of that mathematical expression (Aⁿ), where "A" is known as the base.
It implies that it will raise the base number or the expression to a certain power. Here, "A" is the base, and "n" is the power or exponent.
How to work on the exponents in Python?
There are several ways to calculate the exponents in Python. These are as follows:
Using the double asterisk (**) or exponent operator:
The exponent operator or the power operator operates on two numbers or expressions. These two numbers or expressions combinedly form an exponential number where one is the exponent, and the other is the base. As described above, the exponent signifies the number of times the base number or expression will get multiplied by itself.
Syntax:
m**n
Code:
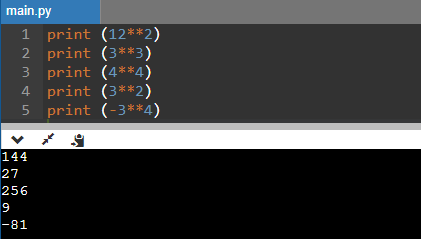
print (12**2)
print (3**3)
print (4**4)
print (3**2)
print (-3**4)
Output:
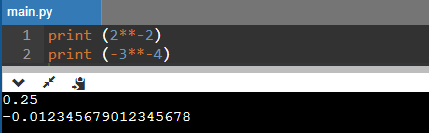
In many cases, when a user wants to raise a negative power, they can use this operator, and the whole expression is inverted. It will look like this:
m**-n == 1/(m**n).
Code Snippet:
print (2**-2)
print (-3**-4)
Output:
Using the pow() function to calculate the exponents:
Python has a built-in function that helps to calculate the power of the number or expression. It has two parameters; that is, a base and an exponent. In the output console, it will return the modulus of the result. The result will always be a positive integer.
Syntax:
pow(m,n)
- exp: It is a number of the expression, which denotes the base of the Python pow() function. It defines the number of times it will calculate the power.
- base: It is a number of the expression; that denotes the exponent of the pow() function, to which it will raise the base.
- mod: A number with which it will compute the modulo.
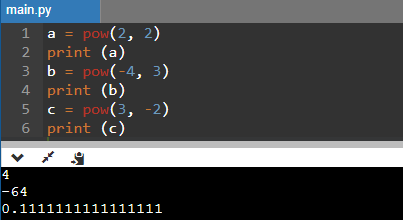
Code:
a = pow(2, 2)
print (a)
b = pow(-4, 3)
print (b)
c = pow(3, -2)
print (c)
Output:
Again, if users want to add a mod argument, such as "c", in pow(a, b, c), the function first performs the task of raising a to the power b, and then it will use the result to perform the modulo task with respect to c. It would be the equivalent of (a**b) % c.
Code:
a = pow(17, 6, 8)
print (a)
b = pow(-20, 3, 13)
print (b)
c = pow(4, 2, -5)
print (c)
Output:

Using the math.pow() function to calculate the exponents:
Python includes another function; called the math.pow() that lets users solve exponents. Like the pow() function, it has two parameters, the base, and the exponent. The primary difference between pow() and math.pow() is math.pow() converts both variables into the floating point and always returns a float, while pow() returns the value in the user-defined data type.
Syntax:
math.pow(m,n)
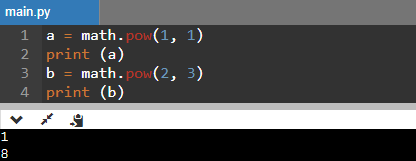
Code Snippet:
a = math.pow(1, 1)
print (a)
b = math.pow(2, 3)
print (b)
Output:
Conclusion:
Users can easily do mathematical calculations in Python, but doing calculations with exponents in Python can be a little tricky. But using the above methods, users can efficiently solve exponents. Also, users should remember that the Python interpreter will return a zero division error if they raise zero to the power of any expression.